This is the accompanying website for the DAFx paper entitled as above. Download the paper here.
Below are sound examples for comparisons between the finite difference schemes on the Cartesian (square) grid using the standard 13-point discrete biharmonic, and on the hexagonal grid using 19-point discrete biharmonic. Another 13-point discrete biharmonic stencil is featured in the paper, but it is left out here.
For more interesting sounds, the lossless model has been extended to the 2-D generalisation of the "stiff string" model, based on [2]. This model includes a "tension" term and frequency-dependent losses. The parameters used are based on Table 1 in [2], although the dimensions of the plate are changed. Here, the plate is circular with a radius of one metre and a thickness of three millimetres. The boundary conditions are of the clamped type.
These are impulse responses using a square grid (left) and a hexagonal grid (right). Both examples use a 33 kHz sample rate.
More high-frequency modes are recovered using the hexagonal grid, but at a greater computational cost. This trade-off is explored in the paper.
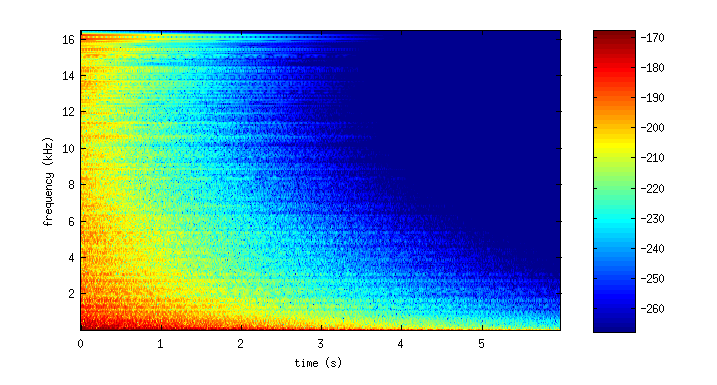
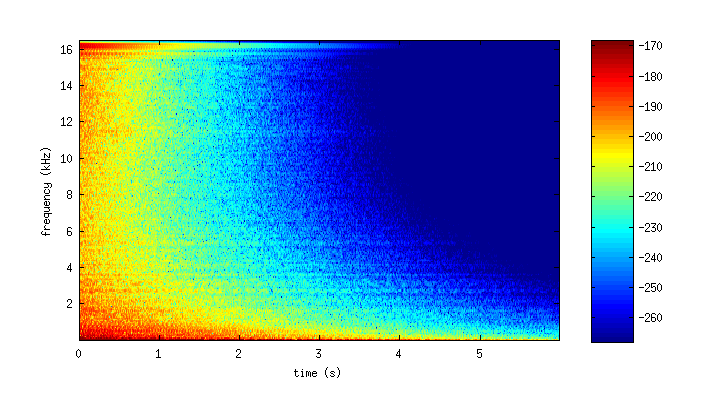
It is worth also investigating the time-frequency behaviour of these sounds. Below are spectrograms for the above examples. The color axis is in decibels.


The output from the square grid (left) results in a sparser modal density in higher frequencies than the output from the hexagonal grid (right).
Below are two animations demonstrating the directional nature of the Cartesian (left) and hexagonal (right) schemes.
B. Hamilton and A. Torin. Finite Difference Schemes on Hexagonal Grids for Thin Linear Plates with Finite Volume Boundaries. Proceedings of the International Conference on Digital Audio Effects (DAFx), Erlangen, Germany, 2014.
S. Bilbao, K. Arcas, and A. Chaigne. A Physical Model for Plate Reverberation. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2006.